はじめに:
 モジュラーデジタイザ (A/Dボード) を使用すると、正確で高解像度のデータをホストコンピュータに迅速に転送・取得できます。デジタイザ (A/Dボード) またはホストコンピュータに適用される信号処理機能により、取得したデータの拡張や単純な測定からの非常に有用な情報の抽出が可能になります。
モジュラーデジタイザ (A/Dボード) を使用すると、正確で高解像度のデータをホストコンピュータに迅速に転送・取得できます。デジタイザ (A/Dボード) またはホストコンピュータに適用される信号処理機能により、取得したデータの拡張や単純な測定からの非常に有用な情報の抽出が可能になります。
Spectrum社のSBench 6や多くのサードパーティプログラムなどの最新のデジタイザサポートソフトウェアには、多くの信号処理機能が組み込まれています。これらには、波形演算、アンサンブルおよびボックスカー平均化、高速フーリエ変換(FFT)、高度なフィルタリング機能、およびヒストグラムが含まれます。
このアプリケーションノートでは、これらすべての機能を調査し、これらのツールの一般的なアプリケーションの典型的な例を示します。
アナログ計算(波形演算):
アナログ計算には、取得した波形の加算、減算、乗算、除算が含まれます。これらの関数は、信号品質を改善するため、または代替関数を導出するためにデータに適用されます。1つの例は、減算を使用して、差動コンポーネントを結合し、コモンモードノイズとピックアップのレベルを低減した差動波形にします。 もう1つは、電流波形と電圧波形の積を使用して瞬時電力を計算することです。
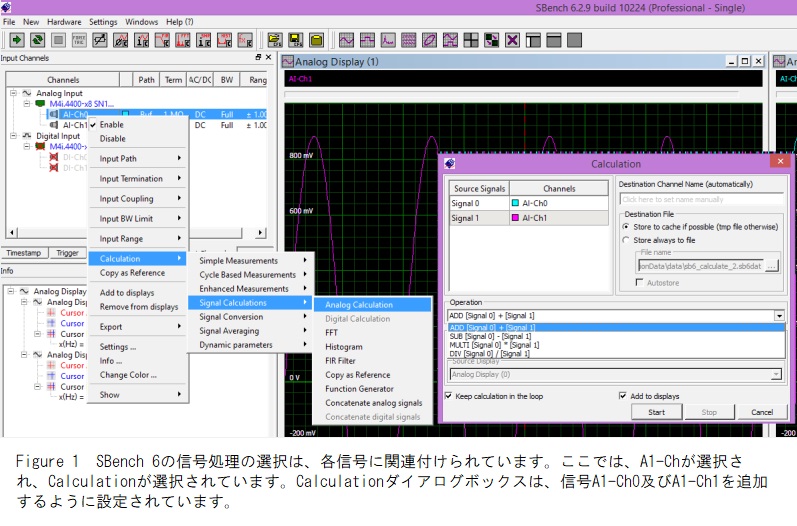
これらの各算術関数は、サンプルごとに波形に適用されます。 これは、結合される波形のレコード長が同じであることを前提としています。 Figure 1は、アナログ計算を選択するためのSBench 6セットアップパスを示しています。目的のソースチャネルを右クリックすると、選択ボックスが表示されます。 [計算]を選択すると、測定、信号計算、信号変換、および平均化に関する追加の選択肢が開きます。信号計算の選択により、高速フーリエ変換(FFT)、ヒストグラム、フィルタリング、その他いくつかの機能にアクセスできます。[アナログ計算]を選択すると、[計算]ダイアログボックスが表示され、目的の算術演算を設定できます。この例では、2つのソース信号が追加されます。他の選択肢は、減算(SUB)、乗算(MULTI)、および除算(DIV)です。 同様の選択パスでその他すべての信号処理機能を立ち上げることができます。
波形演算を適用する最初の例は、1つの信号成分を別の信号成分から減算して差動信号を計算することです。これをFigure 2に示します。
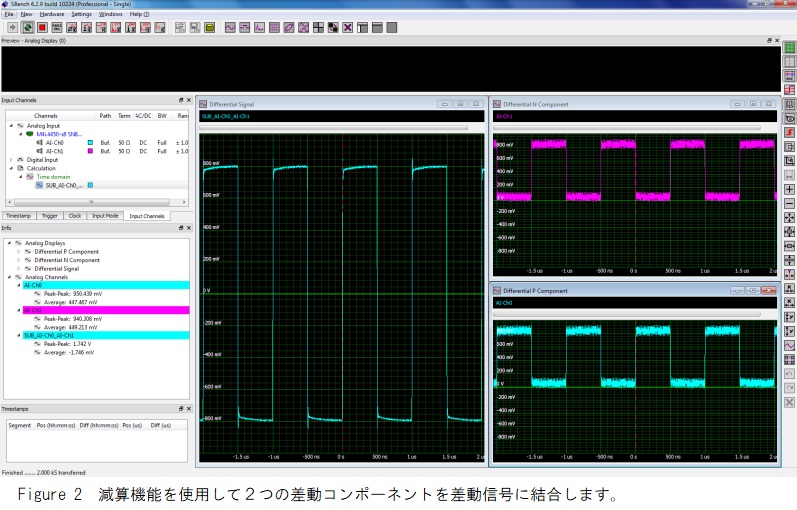
差動信号は、一般的に信号の完全性を向上させるために使用されます。Figure 2の例では、1 MHzクロックの「P」および「N」コンポーネント(右側の2つのパネルに表示)は、減算演算を使用して結合されます。結果の差動信号は、左側のグリッドに表示されます。左中央の情報ペインでは、パラメータを使用して各波形のピークツーピークおよび平均値を測定します。差動信号のピーク間振幅は2倍であり、平均値はほぼゼロであることに注意してください。また、差動部品のコモンモードノイズが除去されていることに注意してください。
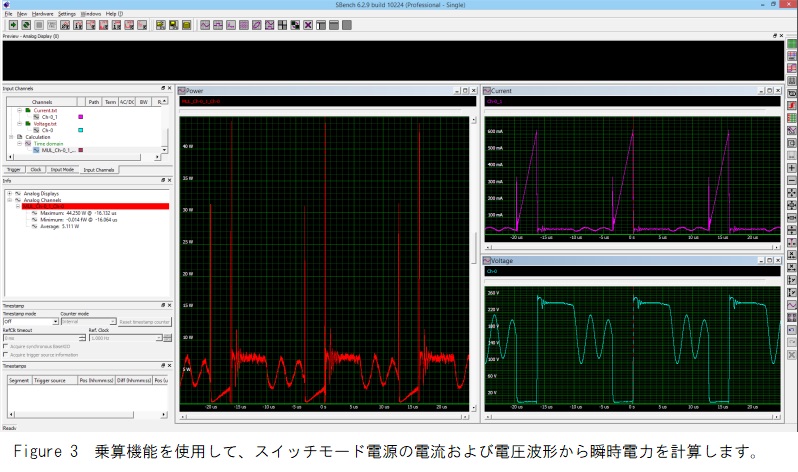
2番目の例では、Figure 3に示すように、電圧波形に電流波形を乗算して瞬時電力を取得します。ソース波形は、パワー電界効果トランジスタ(FET)の電圧と、フライバックモードスイッチング電源のFETチャネル電流です。これらの波形の積は、FETによって消費される瞬時電力を表します。電流波形(右上のグリッド)は、600 mAでピークに達するFET伝導中に直線的に増加するランプを示しています。FETの両端の電圧は導通中は最小ですが、デバイスがオフのときは260 Vのピーク値まで上昇します。 これらの2つの波形の積は、左のグリッドに表示されます。これは、オン(導通)状態とオフ状態の間の遷移中に重大なピークが発生することを示す瞬時電力波形です。 平均(5.111W)およびピーク電力(44.25W)はパラメータを使用して決定され、左中央の情報ペインに表示されます。これらの例は、アナログ計算を使用して、最初に取得した波形から他の重要な波形を導き出す方法を示しています。
平均化:
平均化は、取得した信号に対するノイズと非同期周期波形の影響を低減するために使用される信号処理ツールです。複数の取得と安定したトリガーが必要です。ランダムノイズなど、トリガータイミングと同期していない信号成分の振幅は減少します。削減の程度は、波形の特性と平均に追加される収集の数に依存します。このアプリケーションノートで使用されるSpectrumのSBench 6ソフトウェアとほとんどのオシロスコープは、アンサンブル平均化を実行します。つまり、複数の集録で同じサンプル位置が一緒に平均化されます。安定したトリガーが利用可能な場合、結果の平均には、シングルショットレコードのランダムノイズ成分よりも低いランダムノイズ成分が含まれます。
加算平均:
加算平均は、固定数の集録を使用し連続した波形集録からの同じサンプル位置の同じ重みでの繰り返し加算です。スイープの最大数に達すると、平均化プロセスが停止するか、リセットされて再開します。
Figure 4は、合計アンサンブル平均の概念を示しています:
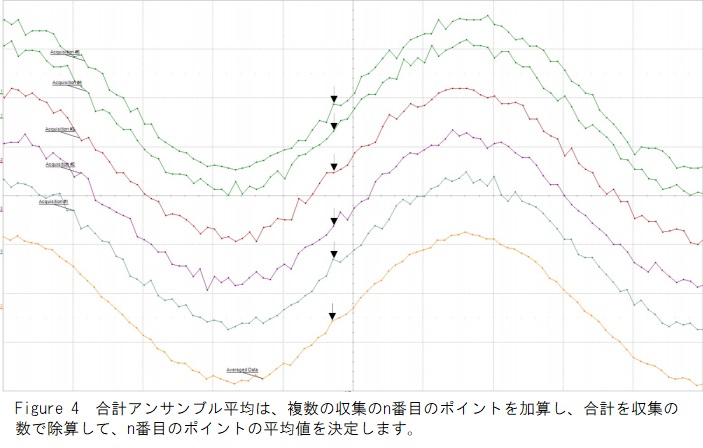
Figure 4では、矢印はn番目のポイントを示しています。各集録のn番目のポイントの振幅値は、他の集録の振幅値と合計されます。次に、合計を取得回数で割って、平均のn番目の値を決定します。これは、収集グループ内のすべてのサンプルポイントに対して行われます。結果の平均化された波形は、取得した各波形と同じ数のポイントを持ちます。平均化は、通常の取得と複数の(セグメント化された)取得の両方でサポートされています。マルチアベレージング計算により、マルチレコーディング取得の連続したセグメントの平均が可能になります。
どのような改善が期待できるのか?:
信号が平均化されると、加法性広帯域ガウスノイズは平均数の平方根だけ減少します。したがって、4つの収集を平均すると信号対雑音比が2対1向上します。同様に、非同期の周期信号は平均で減少します。低減の程度は、取得から取得への干渉信号の位相変動に依存します。歪み成分などのトリガーに同期した信号は、平均化によって振幅が減少することはありません。
平均化の例:
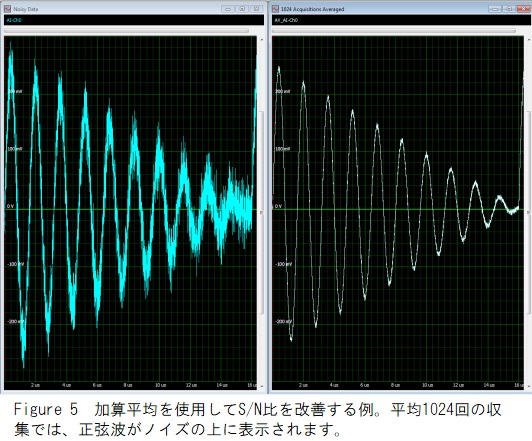
Figure 5は、平均化が役立つ典型的な例を示しています。取得した信号(左のグリッド)は、追加の垂直ノイズを伴う
線形減衰正弦波です。固定振幅ノイズの存在下でサイン振幅が減少すると、ノイズに消えることに注意してください。1024回の収集を平均化すると、S/N比が増加し、正弦波が波形全体で識別できるようになります。合計アンサンブル平均の主な制限は、安定したトリガーを使用して複数の反復波形を必要とすることです。
移動平均:
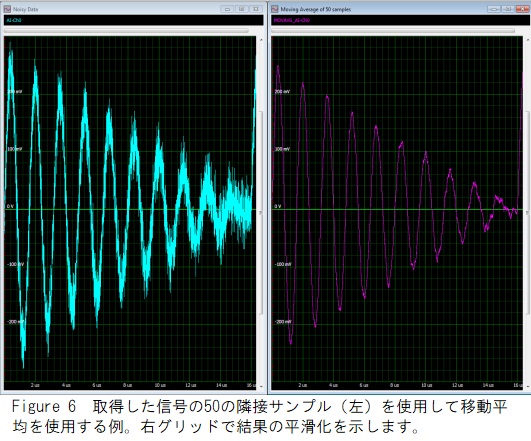
「ボックスカー」平均または平滑化とも呼ばれる移動平均は、対称的に配置された隣接サンプルのユーザー定義数の平均を取ります。サンプルサイズが5の場合、プロセスは次の方程式によって数学的に定義されます:
平均化されたサンプル=
[サンプル(x-2)+サンプル(x-1)+サンプル(x)+サンプル(x + 1)+サンプル(x = 2)] / 5平均で使用されるサンプルの数は、波形の変動の周期に一致する必要があります。そうしないと、移動平均によって狭いフィーチャの振幅が減少する可能性があります。Figure 6は、左側のグリッドに示されている50個の隣接サンプルの移動平均の使用例を示しています。右側のグリッドに表示されている取得された波形と比較したノイズの平滑化と除去に注意してください。サンプルは均一に重み付けされ、平均は取得のサンプルに沿って実行されます。移動平均の利点は、信号を繰り返す必要がないことです。トレードオフは、平滑化された波形を作成する際に、高周波情報の対応する損失があることです。平均化されたサンプル数の設定には注意が必要です。
高速フーリエ変換:
高速フーリエ変換(FFT)は、取得した波形を時間領域(振幅対時間)から周波数領域スペクトル(振幅対周波数)にマッピングします。これにより、信号を構成する周波数成分を観察できます。FFTは信号品質を直接改善しませんが、信号の構造を示し、望ましくないスペクトル成分を除去する方法に関する情報を提供します。時間領域信号に離散時間サンプルがあるように、FFTから生じる周波数スペクトルには離散時間軸があります。多くの場合ビンまたはセルと呼ばれるスペクトル内のサンプルは、取得された信号のレコード長に反比例する分解能帯域幅(f)で間隔が空けられます。そのため、FFTスペクトルの周波数分解能を上げるには、取得した信号のレコード長を増やす必要があります。スペクトル表示の周波数範囲またはスパンは、信号が取得されたサンプルレートの半分です。したがって、スパンを増やすには、サンプリングレートを上げる必要があります。SBench 6のFFTの垂直スケーリングは、ボルトの線形単位またはデシベル(dB)で表される対数単位にすることができます。デシベルスケールは、デジタイザ範囲のフルスケール(dBFS)、1ミリワット(dBm)、1 μV(dbμV)、または変調キャリアと見なされるスペクトルの最大ピーク(dBc)を基準にすることができます。
重み付け関数:
理論的なフーリエ変換は、入力レコードの長さが無限であることを前提としています。レコード長が有限であると、エッジに不連続性が生じる可能性があります。これにより、スペクトル領域に擬似周波数が導入され、実際のスペクトルが歪められます。信号の開始位相と終了位相が異なる場合、信号周波数は2つの周波数ビン内に収まり、スペクトルが広がります。多くの隣接するビンに広がるスペクトルベースの広がりは「漏れ」と呼ばれます。この問題を解決するには、整数の周期が表示グリッド内に含まれるようにするか、エッジに不連続性が表示されないようにします。両方とも、波形信号の周波数とデジタイザ (A/Dボード) のサンプリングレートの間の非常に正確な同期と、測定長の正確な設定が必要です。これは通常、実世界の信号ではなくラボでのみ可能です。もう1つの方法は、ウィンドウ関数(重み付け)を使用して信号のエッジを滑らかにすることです。
これらの影響を最小限に抑えるために、取得した信号に重み関数を適用して、レコードのエンドポイントを強制的にゼロにします。SBench 6のFFTは、ユーザーが8つの重み付け関数のいずれかを選択できるようにします。重み付け関数には、スペクトル線の形状を変更する効果があります。FFTの考え方の1つは、分解能帯域幅で間隔を空けた帯域通過フィルターの並列バンクを合成することです。重み関数は、フィルター周波数応答の形状に影響します。
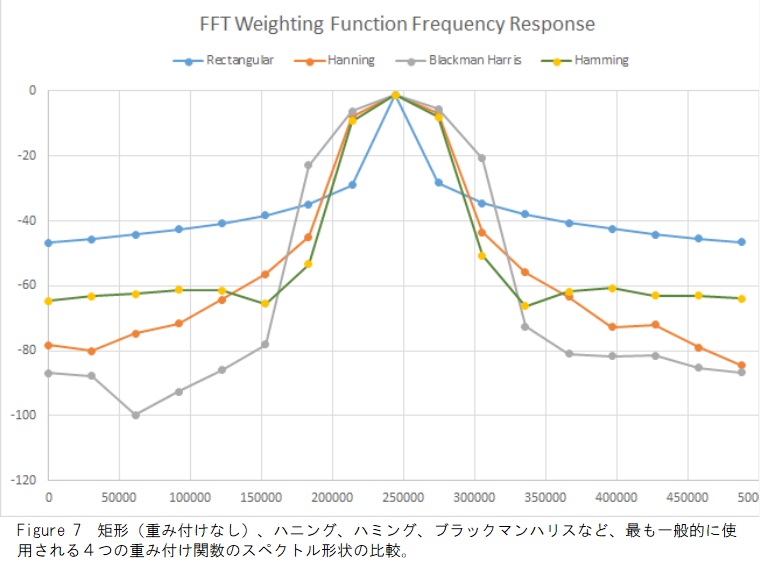
Figure 7は、最も一般的に使用される4つの重み付け関数のスペクトル応答を比較しています。Table 1は、各重み付け関数の主要な特性を示しています。
理想的には、メインローブは真のスペクトル成分を表すために、できる限り狭く平坦でなければなりませんが、すべてのサイドローブは無限に減衰する必要があります。ウィンドウタイプは、FFT処理で使用される同等のフィルターの帯域幅と形状を定義します。スペクトル応答の最大サイドローブ振幅をTable 1に示します。最小のサイドローブレベルは、狭い間隔のスペクトル要素を区別するのに役立ちます。前述のように、FFT周波数軸は分解能帯域幅の倍数で間隔を空けられたビンを持つ離散的です。入力信号の周波数が隣接する2つのビンの間にある場合、エネルギーはビン間で分割され、ピーク振幅が減少します。これは「ピケットフェンス」効果またはスカラップと呼ばれます。スペクトル応答を広げると、振幅変動が減少します。Table 1のスカラップ損失列は、各重み関数の振幅の変動を指定します。
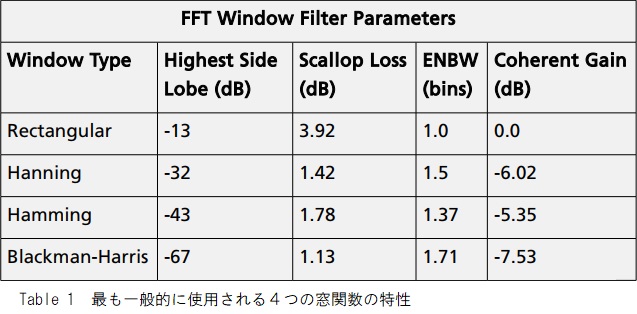
重み付け関数は、スペクトル応答の帯域幅に影響します。有効ノイズ帯域幅(ENBW)は、矩形の重み付けの帯域幅に対する相対的な帯域幅の変化を指定します。パワースペクトルを測定帯域幅(パワースペクトル密度)に正規化するには、パワースペクトルをENBW×分解能帯域幅(f * ENBW)で割る必要があります。コヒーレントゲインは、矩形の重み付けに対する特定の重み付け関数のスペクトル振幅の変化を指定します。これはすべての周波数にわたって固定ゲインであり、簡単に正規化できます。長方形の重み関数は、重みなしの取得信号の応答です。最も狭い帯域幅を持ちますが、かなり高いサイドローブレベルを示します。振幅応答は、取得した時間領域レコードのすべてのポイントにわたって均一であるため、本来過渡的な信号に使用されます(レコード長よりはるかに短い)。また、最高の周波数精度が必要な場合にも使用されます。ハニングおよびハミングの重み付け関数には、適切なサイドローブ応答と共に良好な周波数分解能を提供する、優れた汎用応答があります。Blackman-Harrisは、最高の振幅精度と優れたサイドローブ抑制を目的としています。
FFTアプリケーションの例:
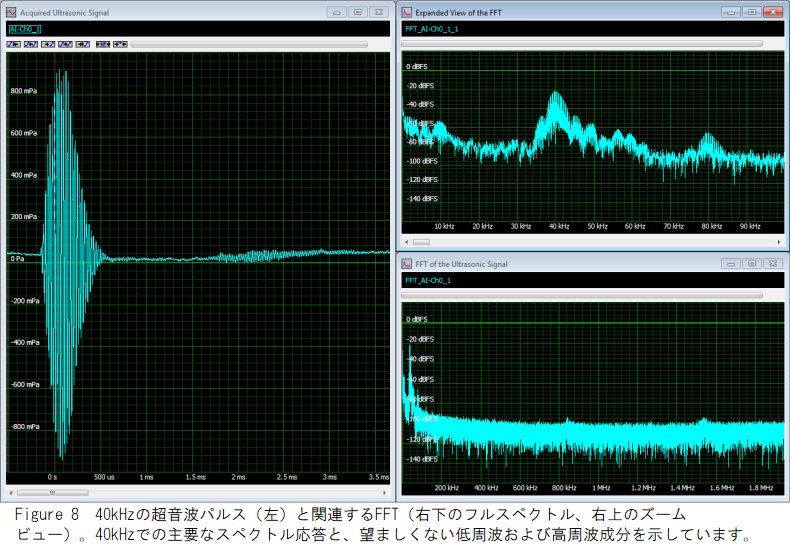
Figure 8は、FFTが役立つ典型的な例を示しています。超音波距離計からの信号は、広帯域計装マイクとSpectrum M4iシリーズ14ビットデジタイザ (A/Dボード) を使用して取得されます。取得した時間領域信号は左側のグリッドにあります。時間領域レコードには、3.90625 MHzのサンプルレートで取得された16,384サンプルが含まれます。継続時間は4.2ミリ秒です。 結果のFFT(右グリッド)は、1.95 MHz(サンプリングレートの半分)のスパンに対して、238 Hzの分解能帯域幅(4.2 msレコード長の逆数)で間隔を空けた8,192個のビンを持ちます。右下のスペクトルはフルスパンです。 右上のズームビューには最初の100 kHzのみが表示され、主要なスペクトル成分をよりよく見ることができます。
FFTにより、この信号を構成する要素をよりよく理解できます。これは、期間が取得したレコード長よりも短い一時的な信号です。この場合、長方形の重み付けが使用されています。 一次信号は40 kHzバーストであり、これは明らかに最大振幅の周波数成分です。40 kHz成分の2次高調波である80 kHz信号があります。その振幅は、40 kHzの信号成分よりも約45 dBです。また、0 Hz~10 kHzの間に多くの低周波成分があります。DC付近の最も高いコンポーネントは、デバイスが使用された部屋で見られる周囲ノイズです。ここでの目標は、送信されたバーストと40 kHzの反射の間の時間遅延を測定できるようにすることです。この測定を改善するために、40 kHz成分の範囲外の信号周波数成分を除去できます。このスペクトルビューは、不要な周波数成分を除去するフィルターを設定する際のガイドになります。
フィルタリング:
SBench 6プロフェッショナルソフトウェアには、ローパス、バンドパス、またはハイパス構成の有限インパルス応答(FIR)デジタルフィルターが含まれています。目的のフィルタータイプ、カットオフ周波数、またはフィルター次数を入力することにより、SBench 6に直接基づいてフィルターを作成できます。SBench 6は、フィルターが実現可能でない場合はアドバイスし、問題を修正する解決策を提案します。
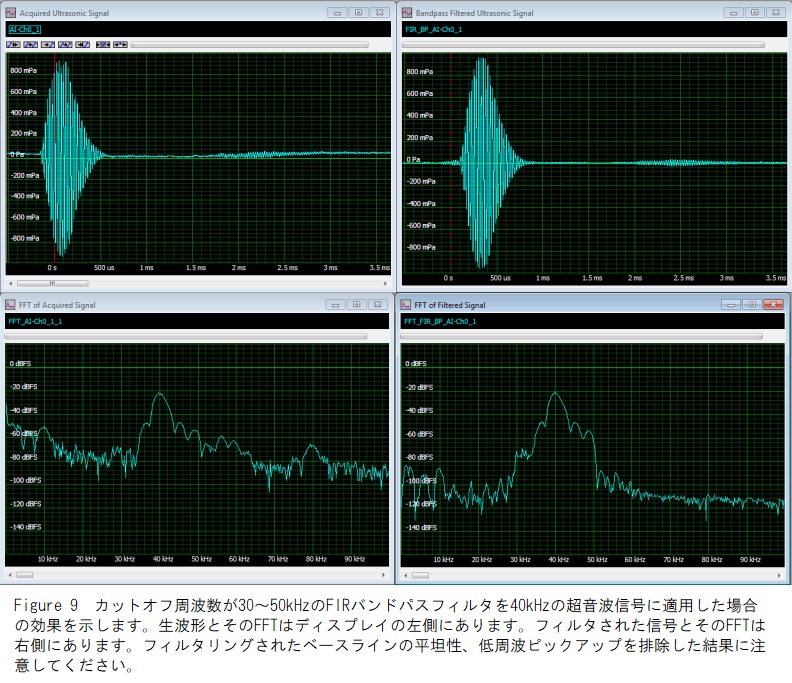
または、別のソースから派生したフィルター係数を入力できます。これらのフィルターは集録された信号に適用でき、結果を生の集録または平均集録と比較できます。Figure 9では、30 kHzと50 kHzのカットオフ周波数を持つFIRバンドパスフィルターが取得した信号に適用されています。左上のグリッドには生の波形が含まれています。その下は、前に見た生信号のFFTです。右上のグリッドには、バンドパスでフィルタリングされた波形が含まれています。フィルタリングされた信号のFFTは、右下のグリッドにあります。バンドパスフィルターにより、低周波ピックアップと80 kHzの2次高調波が除去されていることに注意してください。フィルター処理された信号の時間ドメインビューは、ベースラインがフラットになりました。反射はより明確に識別可能であり、これが処理の目標です。繰り返しますが、FFTはフィルタリングプロセスに関する優れた洞察を提供します。
ヒストグラム:
これまで、時間領域と周波数領域の両方でデータを見てきました。これらの各ビューは、取得するデータの理解に何かを追加します。特定の振幅値が発生する確率を扱う統計領域のデータを表示することもできます。これは、発生頻度対振幅値をプロットするヒストグラムによって伝えられます。ヒストグラムは、信号の確率分布の有限レコード長の推定値です。SBench 6は、取得した波形のヒストグラムを作成する機能を提供します。
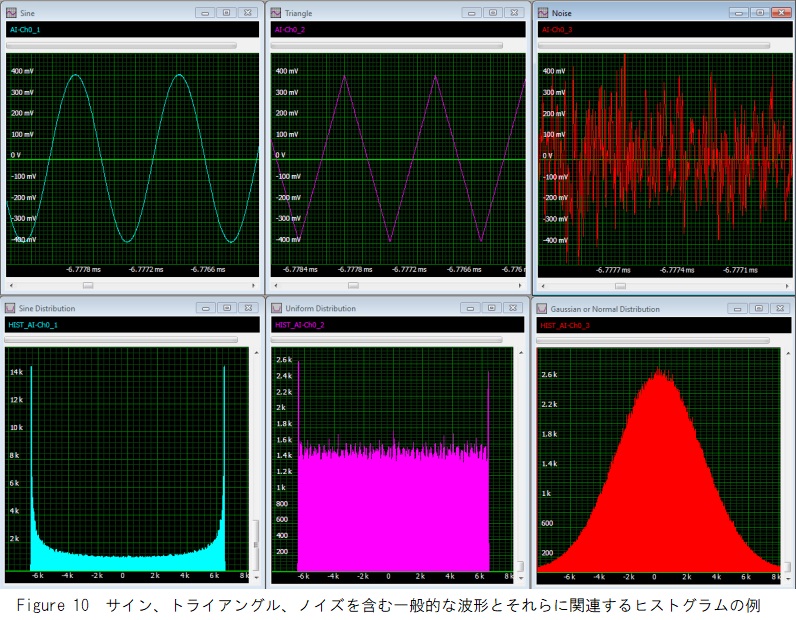
Figure 10に、正弦波、三角波、ノイズ波形、およびそれらに関連するヒストグラム分布を含むいくつかの例を示します。波形の一番上の行には、正弦波、三角波、ノイズ波形が表示されます。それらの下には、関連するヒストグラムがあります。ヒストグラムの横軸は、信号の振幅を表します。縦軸は、小さな値の範囲内の値の数を示します(ビニング)。各ヒストグラム分布は明確であり、その差は信号特性に関連しています。正弦波の分布は、極値とand型の中間領域のいずれかで高いピークを示しています。このシェーピングの理由は、正弦波の変化率が各サイクルで変化するためです。ゼロクロッシングで最も高く、ピークで最も遅くなります。サインが均一なサンプリングレートでサンプリングされる場合、正(ヒストグラムの右端のピーク)と負(左端のピーク)のサンプルが多くなり、ゼロ交差(ヒストグラムの中央に水平方向)のサンプルが最も少なくなります。三角波には、正または負の一定の勾配があります。結果のヒストグラムは、極端な場合を除き、均一な分布になります。ピークが存在するのは、信号発生器の帯域幅が制限されており、ピークが丸められそれらのポイントでより多くのサンプルが取得されるためです。
ノイズ信号のヒストグラムは、ガウス分布または正規分布になります。おそらく、統計コースを受講した人にとっては、その配布にあまり時間をかける必要はないでしょう。ガウス分布のユニークな特徴は、制限されていないことです。他の分布には振幅制限があり、水平範囲は固定されています。ガウス分布には、理論的に無限に広がる「テール」があります(実際の機器では、テールはアナログからデジタルへのコンバーターのクリッピングによって制限されます)。そのため、ヒストグラムは、取得した信号に関する独自のストーリーを伝えます。それらは、波形の非対称性(歪み)と低確率の「グリッチ」を示すのに適しています。
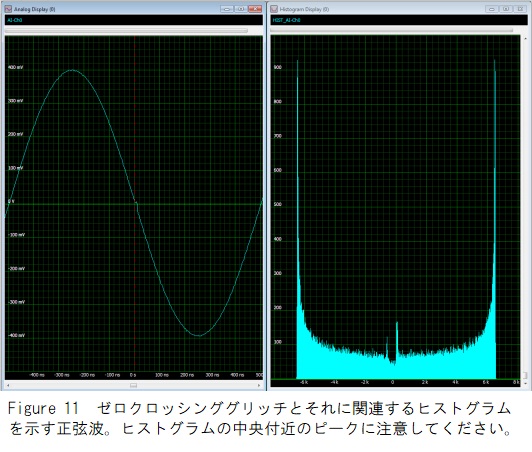
Figure 11に、ゼロ交差にグリッチがある正弦波のヒストグラムを示します。ヒストグラムは、Figure 10の正弦ヒストグラムには存在しないゼロ交差付近の重要なピークを明確に示しています。
まとめ:
アナログ計算、平均化、FFT、フィルタリング、ヒストグラムなどの信号処理ツールは、取得したデータを解釈し、データの詳細な洞察をもたらす二次信号を導き出します。
——————————————————————–
原文ドキュメント:Spectrum Instrumentation社
an_signal_processing_for_digitizers_0.pdf
Signal Processing for Digitizers
関連製品
M4i.4421-x8:250MHz A/D ボード (PCIe)
M4i.4451-x8:500MHz 高速A/D ボード (PCIe)
M4i.4471-x8:180MHz A/D ボード (PCIe)
Spectrum Instrumentation社について
Spectrum社は、Spectrum Systementwicklung Microelectronic GmbHとして1989年に設立され、2017年にSpectrum Instrumentation GmbHに改名されました。最も一般的な業界標準(PCIe、LXI、PXIe)で500を超えるデジタイザおよびジェネレータ製品を作成するモジュール設計のパイオニアです。これら高性能のPCベースのテスト&メジャーメントデザインは、電子信号の取得・生成および解析に使用されます。同社はドイツのGrosshansdorfに本社を置き、幅広い販売ネットワークを通じて世界中に製品を販売し、設計エンジニアによる優れたサポートを提供しています。 Spectrum社の詳細については、www.spectrum-instrumentation.comを参照してください。

